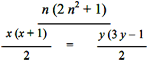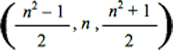QSA Members Forum
For Masonic Research
The Sacred Numbers in the Masonic Pythagorean Tradition
English Translation
of the Book
Titled
 I Numeri Sacri Nella Tradizione Pitagorica Massonica
I Numeri Sacri Nella Tradizione Pitagorica Massonica
(The Sacred Numbers in the Masonic Pythagorean Tradition)
Translated by Bro. Vincent Lombardo.
![]()
Translator's Note:
The original contents of this presentation have been taken from the document of the same title published in the Ifremer website, pursuant to its Legal notice/Credit, Section: "Droits accordés" [Granted rights], specifically:
Droits accordés
"L'Ifremer accorde à l'utilisateur un droit personnel, gratuit, non exclusif et non transférable d'accès et d'utilisation de son site Internet. Tout autre droit est expressément exclu.
En conséquence, et de manière non exhaustive, les droits de (i) reproduire, représenter, adapter et/ou traduire, (ii) extraire, ou (iii) de créer tout travail dérivé de tout ou partie du site Internet de l'Ifremer et/ou de contenus y afférent, sont formellement et strictement interdits en dehors du cadre strictement limité à l'exception de copie privée ou à visée éducative."
Dans les cas de copie privée ou à visée éducative, toute reproduction par l'utilisateur de données doit s'accompagner, de manière lisible et claire, de la mention suivante: «ce document est extrait du site Internet de l'Ifremer. Informations protégées - Tous droits réservés © Ifremer (2010/05/239469677)». That is: this document is taken from the Ifremer website. Protected information - All rights reserved © Ifremer (2010/05/239469677)
Si Noti: questa pagina è ottimizzata per Google Chrome (al 150%).
Please note: this page is best viewed with Google Chrome (Zoomed at 150%)

|
INDEX
|
INDICE
|

|
NOTE FROM THE CURATOR, Graziano Gamba "The Florentine mathematician and scholar Arturo Reghini (1878-1946), a high dignitary of Freemasonry before its dissolution at the hands of fascism, was the best-known exponent of neo-Pythagoreanism in the twentieth century, and a theorist of "Pagan imperialism." A Friend of Giovanni Amendola and of Giovanni Papini, a leading figure of the Florentine scapigliatura at the time of the magazines "Leonardo," "Lacerba" and "La Voce," he was, in turn, the founder of the magazines "Atanòr" (1924), "Ignis" (1925 ) and - with Julius Evola - "UR" (1927-1928). Linked to his work are the revival of "cultured magic", neo-Platonic and Renaissance, which he opposed to Christianity as a gateway to the divine, and a radical critique of modern occultism and pseudo-esotericisms. In collaboration with René Guénon, he hoped for the spiritual rebirth of the West through the formation of an initiatory elite in the framework of a process of regeneration of Freemasonry, in which he saw a "deviated" residue of an ancient Hermetic-Pythagorean organization, of pre-Christian origin and heir of the ancient Mysteries. Most effective polemicist; he was an interventionist and advocate of early fascism, but broke with Mussolini at the time of the Matteotti assassination and, with the establishment of the dictatorship, he retired to the study of Pythagorean geometry and mathematics. Already in his life, a substantial legend of "magician" and prodigy maker had formed on his account, enriched over time with other imaginative additions." |
NOTA DEL CURATORE, Graziano Gamba «Il matematico ed erudito fiorentino Arturo Reghini (1878-1946), alto dignitario della Massoneria prima del suo scioglimento ad opera del fascismo, fu il più noto esponente del neo-pitagorismo nel XX secolo e teorico dell'"lmperialismo Pagano". Amico di Giovanni Amendola e di Giovanni Papini, personaggio di punta della scapigliatura fiorentina all'epoca delle riviste "Leonardo", "Lacerba" e "La Voce", fu a sua volta fondatore delle riviste "Atanòr" (1924), "Ignis" (1925) e - con Julius Evola - "UR" (1927-1928). Alla sua opera sono legate la riproposizione della "magia colta", neo-platonica e rinascimentale, che contrappose al Cristianesimo come via d'accesso al divino, ed una critica radicale dell'occultismo e degli pseudo-esoterismi moderni. In collaborazione con René Guénon, auspicò la rinascita spirituale dell'Occidente attraverso la formazione di un'élite iniziatica nel quadro di un processo di rigenerazione della Massoneria, in cui vedeva un residuo "deviato" di un'antica organizzazione ermetico-pitagorica, d'origine pre-cristiana ed erede degli antichi Misteri. Polemista efficacissimo; fu interventista e fautore del primo fascismo, ma ruppe con Mussolini all'epoca del delitto Matteotti e con l'instaurazione della dittatura, ritirandosi nello studio della geometria e della matematica pitagoriche. Già in vita, sul suo conto s'era formata una corposa leggenda di "mago" e di facitore di prodigi, arricchitasi con il tempo di altre fantasiose aggiunte». |
|
ARTURO REGHINI THE SACRED NUMBERS IN THE MASONIC PYTHAGOREAN TRADITION Premises Freedom he is seeking, for so dear it is According to what the ancient rituals and the ancient Masonic constitutions unanimously affirm, Freemasonry has as its goal the perfecting of man. The traditionally correct conception is certainly the first one, and in the Masonic literature of two centuries ago there was a great vogue for exaggerated and imaginative approaches and identifications of the Masonic with the Eleusinian Mysteries. Without a doubt, the ritualistic and symbolic patrimony of the Masonic Order is in harmony only with the most ancient conception of the goal of Freemasonry; in fact, the testament of the initiate, the symbolic journeys [perambulations], the terrible trials, the birth in the initiatory light, the death and resurrection of Hiram, it is not clear what relationship they may have with the Masonic works and with the purpose of Freemasonry if everything is to be reduced to make politics. Now, it is very important to note that the Anderson Constitutions explicitly state that, to be initiated and belong to Freemasonry, one only needs to be a free man and of good morals, exalting (unlike the various Christian sects) the principle of mutual tolerance of each brother for the beliefs of others, adding only that a Mason will never be a "stupid atheist." Someone may perhaps think that Anderson admits that the Mason may be an intelligent atheist, but it is more likely that Anderson, as a good Christian, admits that an atheist is necessarily a fool, following the maxim that says: Dixit stultus in corde suo: Non est Deus [The fool has said in his heart: there is no god]. It would be necessary here to digress and observe that, in this dispute, both the one affirming and the one denying have in general no notion of what they claim to exist or not, and that the word God is usually used with such an indeterminate meaning as to make any discussion useless. However, the Constitutions of Freemasonry are explicitly theistic; and those profane who accuse Freemasonry of atheism are in bad faith or are unaware that it works for the glory of the Great Architect of the Universe; and we observe again that this designation, besides being in harmony with the character of the masonic symbolism, has a precise and intelligible meaning, unlike other vague or meaningless designations such as that of "Our Lord", of "Father of all men," etc. The fundamental character of the Anderson Masonic Constitutions lies, therefore, in the principle of freedom of conscience and tolerance, which also makes it possible for non-Christians to belong to the Order. In the Constitutions of Anderson, Freemasonry retains its universal character, is not subordinate to any particular philosophical belief or any religious sect, and does not show any tendency to work of a social and political nature; it may be that this non-denominational and free character also inspired Freemasonry before 1717, and that Anderson did nothing but sanction it in the Constitutions. On the other hand, it must be recognized that, if the Anglo-Saxon Freemasonry has always maintained the spiritualist character and has never thought of declaring the inexistence of the Great Architect of the Universe, it has often been inclined, and still is, to confer a Christian color to his spiritualism, moving away from the spirit of absolute impartiality and non-denomination of the Anderson Constitutions. It cannot be denied that imposing the oath on the Gospel of St. John is a manifestation that is not too tolerant with respect to those profane and those brothers who, being agnostics, or pagans, or Jews or free thinkers, do not feel particular sympathy for the Gospel of San Giovanni, and they know nothing of the Johannite tradition. The intolerance is accentuated with the habit of inflicting the reading and commenting of verses from the Gospel during the work of the Lodge. This ill habit, if it were to be affirmed, would reduce the work of the Lodge to the level of a service of a Quaker or Puritan church, to a sort of annoying, inconclusive and repulsive rosary and vespers to the free conscience of the many brothers who, even in England, and in America, not only do they not go to mass, and do not accept the infallibility of the Pope, but they no longer even accept the authority of the Bible. Is it worthwhile to provoke discomfort and intolerance between the columns without significant compensation? Do you believe by such means to convert others to your belief, and to stem the powerful wave of English and American agnosticism? This critique affirms that absolute emptiness is contained in the depth of the secret tradition (page 139) and concludes with the affirmation that "the Initiatory School, or for it, the Secret Tradition, has taught humanity absolutely nothing" (page 155). It is really not clear how we can then also affirm that this absolute emptiness, "this secret tradition coincides, (p. 141), albeit often in a corrupt form, with the Gnostic doctrines," but we do not expect too much. Freemasonry is, therefore, according to the author, a sphinx with no secret because it does not teach any doctrine, and the reader is thus led to conclude that Freemasonry, being devoid of content, is worth nothing. In the foregoing we have shown that Freemasonry does not pursue any doctrine and must not teach any; and that this is a merit and not a demerit of Freemasonry. To then conclude that, not containing a doctrine, the secret Tradition contains absolute emptiness, we must believe that only a doctrine can fill the emptiness. Del Castillo affirms again (page 153) that "the initiatory system supposes that man can come to understand with the effort of the brain the unsolved problems of the cosmos and beyond"; and that the "Catholic Church (p. 156) opposes to the vain reflections of the so-called initiates the intangible force of its dogma, which must be unique because there cannot be two truths"; and that the initiatory system (p. 152) is incompatible with Christianity. To these and similar affirmations we reply that we are ignorant of the existence of an initiatory system, that we do not know initiates who make assumptions, much less who delude themselves that they can understand unsolved problems with their brains alone and with lucubrations: but it is not possible for us to admit that faith in a dogma constitutes knowledge - because knowing is not believing. On the contrary, we understand that truth is necessarily ineffable and indefinable, and we leave to the layman the naive and consoling illusion that any formulation of truth and knowledge is possible [by means] of creeds, formulas, doctrines, systems, and theories. After all, Jesus too knew that his parables were nothing but parables, but he also told his disciples that "they were given to understand the mystery of the kingdom of heaven." Evidently, sola fides sufficit ad firmandum cor sincerum [faith alone is sufficient to strengthen a sincere heart], but it is not enough to understand the mysteries. The same naturally applies to reasoning alone. And by this we do not intend to impair the value of faith and reasoning; faith alone leads to ignorant fanaticism; reasoning alone leads to philosophical despair; they are a bit like tobacco and coffee: two poisons that compensate for each other; but, of course, it is not enough to smoke a pipe and sip coffee to gain knowledge. To knowledge multi vocati sunt [many are called to], not all; and, among these many, pauci electi sunt [only a few are chosen]; according to the Catholic Church, however, faith in Dogmas is sufficient, and knowledge and paradise are within the reach of all purses at competitive prices. It is therefore not surprising that the freemasons identified the art of architecture with the science of geometry and gave the knowledge of numbers such importance as to justify their traditional claim of being the only ones to have the knowledge of "sacred numbers." This Platonic conception and attitude is the same that is found in the Italic or Pythagorean school that exercised a great influence over Plato, so that even if we want to argue that Freemasonry was inspired by Plato, it has always been ultimately traced back to geometry and arithmetic of the Pythagoreans. The link between Freemasonry and the Pythagorean Order, even if it is not an uninterrupted historical derivation, but only a spiritual filiation, is certain and manifest. The archpriest Domenico Angerà, in the 1874 preface to the reprint of the General Statutes of the Society of Freemasons of the Ancient and Accepted Scottish Rite, already published in Naples in 1820, categorically states that the Masonic Order is the same, the very same thing as the Pythagorean Order; but even without going so far, the affinity between the two orders is certain. In particular, the geometric art of Freemasonry derives, directly or indirectly, from Pythagorean geometry and arithmetic; and no further, because the Pythagoreans were the creators of these liberal sciences, according to what appears historically, and according to the attestation of Proclus. With the exception of a few geometric properties attributed, probably wrongly, to Thales, geometry, says Tannery, springs complete from the genius of Pythagoras as Minerva leaps fully armed from the brain of Jupiter; and the Pythagoreans were the first to begin the study of arithmetic and numbers. |
ARTURO REGHINI I NUMERI SACRI NELLA TRADIZIONE PITAGORICA MASSONICA Premesse Libertà va cercando ch'è sì cara Secondo quanto affermano concordemente gli antichi rituali e le antiche costituzioni massoniche, la Massoneria ha per fine il perfezionamento dell'uomo. La concezione tradizionalmente corretta è sicuramente la prima, e nella letteratura massonica di due secoli fa ebbero grande voga esagerati e fantasiosi avvicinamenti ed identificazioni dei misteri eleusini e massonici. Senza ombra di dubbio il patrimonio ritualistico e simbolico dell'Ordine muratorio è in armonia soltanto con la concezione più antica del fine della massoneria; infatti il testamento dell'iniziando, i viaggi simbolici, le terribili prove, la nascita alla luce iniziatica, la morte e resurrezione di Hiram, non si capisce quale relazione possano avere coi lavori massonici e con lo scopo della Massoneria se tutto si deve ridurre a fare della politica. Ora è molto importante notare che le Costituzioni dell'Anderson affermano esplicitamente che per essere iniziato ed appartenere alla Massoneria si richiede solo di essere un uomo libero e di buoni costumi, ed esaltando (a differenza delle varie sette cristiane) il principio della tolleranza reciproca di ogni fratello per le altrui credenze, aggiungendo solo che un massone non sarà mai uno «stupido ateo». Taluno potrà forse pensare che l'Anderson ammetta che il massone possa essere un ateo intelligente, ma è più verosimile che l'Anderson da buon cristiano ammetta che un ateo è necessariamente uno stupido, seguendo la massima che dice: Dixit stultus in corde suo: Non est Deus. Bisognerebbe qui fare una digressione ed osservare che in questa disputa tanto chi afferma quanto chi nega non ha in generale nozione alcuna di quanto afferma esistere o no, e che la parola Dio viene adoperata di solito con un senso talmente indeterminato da rendere vana qualunque discussione. Comunque le Costituzioni della Massoneria sono esplicitamente teistiche; e quei profani che accusano la Massoneria di ateismo sono in mala fede od ignorano che essa lavora alla gloria del Grande Architetto dell'Universo; ed osserviamo ancora che questa designazione oltre ad essere in armonia col carattere del simbolismo muratorio ha un significato preciso ed intelligibile a differenza di altre designazioni vaghe o prive di senso come quella di «Nostro Signore», di «Padre di tutti gli uomini» ecc. Il carattere fondamentale delle Costituzioni massoniche dell'Anderson sta adunque nel principio della libertà di coscienza e della tolleranza, che rende possibile anche ai non cristiani di appartenere all'Ordine. Nelle Costituzioni dell'Anderson la Massoneria conserva il suo carattere universale, non è subordinata ad alcuna credenza filosofica particolare né ad alcuna setta religiosa, e non manifesta alcuna tendenza a lavori di ordine sociale e politico; può darsi che questo carattere aconfessionaJe e libero inspirasse anche la Massoneria anteriore al 1717 e che l'Anderson non abbia fatto altro che sancirlo nelle Costituzioni. D'altra parte bisogna riconoscere che, se la massoneria anglosassone ha sempre mantenuto il carattere spiritualista e non ha mai pensato a dichiarare la inesistenza del Grande Architetto dell'Universo, essa è stata spesso incline, e lo è ancora, a conferire un colorito cristiano al suo spiritualismo, allontanandosi dallo spirito di assoluta imparzialità ed aconfessionalità delle Costituzioni dell'Anderson. Non si può negare che l'imporre il giuramento sul Vangelo di San Giovanni sia una manifestazione non troppo tollerante rispetto a quei profani ed a quei fratelli che, essendo agnostici, o pagani, od ebrei o liberi pensatori, non sentono particolare simpatia per il Vangelo di San Giovanni e non sanno nulla della tradizione gioannita. L'intolleranza si accentua con l'andazzo di infliggere la lettura ed il commento di versetti del Vangelo durante i lavori di Loggia. Questo mal vezzo, qualora si affermasse, ridurrebbe i lavori di Loggia al livello di un service di una chiesa quacchera o puritana, ad una specie di rosario e vespro fastidioso, inconcludente, e ripugnante alla libera coscienza dei moltissimi fratelli i quali, anche in Inghilterra, ed in America, non solo non vanno alla messa, e non accettano l'infallibilità del Papa, ma non accettano più neppure l'autorità della Bibbia. Vale la pena di provocare il disagio e l'insofferenza tra le colonne senza sensibile compenso? Si crede proprio con simili mezzi di convertire gli altri alla propria credenza, e di arginare la potente ondata dell'agnosticismo inglese ed americano? Questa critica afferma che nel fondo della tradizione segreta è contenuto il vuoto assoluto (pag. 139) e conclude con l'affermare che «la Scuola Iniziatica o per essa la Tradizione Segreta, non ha insegnato assolutamente nulla all'umanità» (pag. 155). Veramente non si capisce bene come si possa allora anche affermare che questo vuoto assoluto, «questa tradizione segreta coincide (pag. 141), se pure spesso in forma corrotta, con le dottrine gnostiche», ma non pretendiamo troppo. La Massoneria è dunque, secondo l'autore, una sfinge senza segreto perché non insegna alcuna dottrina, ed il lettore è così portato a concludere che essendo priva di contenuto la Massoneria non val niente. In quanto precede noi abbiamo mostrato che la Massoneria non insegua alcuna dottrina e non deve insegnarne; e che questo è un merito e non un demerito della Massoneria. Per concludere poi che, non contenendo una dottrina, la Tradizione segreta contiene il vuoto assoluto bisogna credere che soltanto una dottrina possa occupare il vuoto. Afferma ancora (pag. 153) il Del Castillo che «il sistema iniziatico suppone che l'uomo possa arrivare a capire con lo sforzo del cervello i problemi insoluti del cosmo e dell'al di là»; e che la «Chiesa cattolica (pag. 156) oppone alle vane elucubrazioni dei così detti iniziati la forza intangibile del suo dogma che deve essere unico perché non possono esistere due verità»; e che il sistema iniziatico (pag. 152) è incompatibile can il cristianesimo. A queste e simili affermazioni rispondiamo che ignoriamo la esistenza di un sistema iniziatico, che non conosciamo iniziati che facciano delle supposizioni, e tanto meno che si illudano di potere capire col solo cervello e con elucubrazioni di problemi insoluti: ma non ci è possibile ammettere che la fede in un dogma costituisca una conoscenza perché sapere non è credere. Anzi noi comprendiamo che la verità è necessariamente ineffabile ed indefinibile, e lasciamo ai profani l'ingenua e consolante illusione che sia possibile una qualsiasi formulazione della verità e della conoscenza in credi, formule, dottrine, sistemi e teorie. Anche Gesù, del resto, sapeva che le sue parabole non erano che delle parabole, ma diceva anche ai suoi discepoli che ad essi «era dato intendere il mistero del regno dei cieli». Evidentemente sola fides sufficit ad firmandum cor sincerum, ma non sufficit per intendere i misteri. Lo stesso dicasi naturalmente per il solo raziocinio. E con questo non intendiamo menomare il valore della fede e del raziocinio; la sola fede conduce al fanatismo ignorante, il solo raziocinio conduce alla disperazione filosofica; sono un po' come il tabacco ed il caffè: due veleni che si compensano; ma naturalmente non basta fumare la pipa e centellinare il caffè per assurgere alla conoscenza. Alla conoscenza multi vocati sunt, non tutti; e, tra questi molti, pauci electi sunt; secondo la Chiesa cattolica invece basta la fede nel Dogma, e conoscenza e paradiso sono alla portata di tutte le borse a prezzi di vera concorrenza. Non stupisce quindi che i liberi muratori identificassero l'arte architettonica con la scienza della geometria e dessero alla conoscenza dei numeri tale importanza da giustificare la loro pretesa tradizionale di essere i soli ad avere conoscenza dei «numeri sacri». Questa concezione ed attitudine di Platone è la medesima che si ritrova nella scuola Italica o pitagorica che esercitò sopra Platone grandissima influenza, di modo che anche volendo sostenere che la Massoneria si sia inspirata a Platone, si è sempre in ultima analisi ricondotti alla geometria ed all'aritmetica dei pitagorici. Il legame tra la Massoneria e l'Ordine pitagorico, anche se non si tratta di ininterrotta derivazione storica, ma soltanto di filiazione spirituale, è certo e manifesto. L'Arciprete Domenico Angherà nella prefazione del 1874 alla ristampa degli Statuti Generali della Società dei Liberi Muratori del Rito Scozzese Antico ed Accettato, già pubblicati in Napoli nel 1820, afferma categoricamente che l'Ordine massonico è la stessa, stessissima cosa dell'Ordine pitagorico; ma anche senza spingersi tanto oltre l'affinità tra i due ordini è sicura. In particolare l'arte geometrica della Massoneria deriva, direttamente od indirettamente, dalla geometria ed aritmetica pitagoriche; e non più in là, perché i pitagorici furono i creatori di queste scienze liberali, a quanto risulta storicamente e secondo la attestazione di Proclo. Ad eccezione di alcune poche proprietà geometriche attribuite, probabilmente a torto, a Talete, la geometria, dice il Tannery, scaturisce completa dal genio di Pitagora come Minerva balza armata di tutto punto dal cervello di Giove; ed i pitagorici sono stati i primi ad iniziare lo studio dell'aritmetica e dei numeri. |
|
CHAPTER I The Pythagorean Tetractis and the Masonic Delta No, I swear it by he who has transmitted Exhuming and restoring the ancient Pythagorean arithmetic is a very difficult task, because the information that remains of it is scarce and not all reliable. We should at every step and statement cite sources and discuss their value, but this would make our exposure long and heavy and difficult to understand. Therefore, in general, we will abstain from any philology, we will stick only to what has been resulted less controversial and always declare where it is just our opinion or our work. In Modern times, however, it has been noted that 1, 2, 3 are the only positive integers whose sum is equal to the product. It can also be easily recognized that 1, 2, 3 is the only triplet of consecutive integers for which it happens that the sum of the first two is equal to the third; in fact, the equation x + (x + 1) = x + 2 admits x = 1 as the sole solution. Thus, it is also immediately recognized through the geometric representation that the sum of several consecutive integers always exceeds the number that follows the last of the addends, except in the case in which the addends are two where we have: 1 + 2 = 3. In conclusion, the triad, the holy trinity, can only be obtained through the addition of the monad and the dyad.
This geometric development of the first triangle with respect to one of the three vertices, taken as the center of homothety, gives us thus successively the triangular numbers; and the base that is added to pass from a triangular to a consecutive triangular is called a triangular gnomon. Arithmetically, once the succession of integers is written in a first line, the succession of triangles is deduced, writing the unit under the unit, then making the sum of one and two, and then taking as elements of the second line the numbers that are obtained by successively making the sum of the first integers, or by making, to obtain an element of the second row, the sum of the element that precedes it in the same row with the one that precedes it in the same column:
It is therefore a square; is the second square, because the unit is the square of one. The gnomon of the square, i.e., the difference between the 4 which is the second square and the previous square is 3, the third square, that is, as we say the square of base 3, is obtained in the geometric representation by adding one below and to the right squad-shaped gnomon consisting of 5 points; and so on, you move from one square to the next by adding the odd numbers successively. Thus we see that even the squares grow while maintaining the similarity of the form; and, since four congruent right angles can be arranged around a point and a square in each of them, it follows that, by homothetically developing the four squares with respect to the common vertex as homothetic center, the total and isotropic coverage of the plane is obtained by means of squares.
By leading a straight line to the side and parallel to a diagonal it divides a heteromecic number into two parts, that are two equal triangles; and as the number of points of the heteromecic n°, consisting of n columns and n rows is n (n + 1) it follows for the triangular number n° the following formula:
Recalling the definition of triangular we have
If, on the other hand, one leads the parallel to a diagonal in a square number, the square is divided into two consecutive triangles; that is, the sum of two consecutive triangles is equal to a square; and this allows us to deduce from the succession of triangles that of squares. Written in the first row the succession of triangles, the succession of squares is obtained in the second row There is only one linear development of numbers. There are, however, an infinite number of surface developments and solid developments. For example, the number 5 can be represented in the plane by means of the 5 vertices of a pentagon and in space by the five vertices of a square-based pyramid. The development for all pentagons is made by taking one of the vertices of the pentagon as the homothetic center, and for the square-based tetrahedron, by taking the apex of the pyramid as the homothetic center. Arithmetically, to obtain the pentagonal series is enough to start from the succession of the terms of the arithmetic series of three, that is to say from the numbers: 1, 4, 7, 10, 13, 16 … and make the sum of them. The sum of the first n is equal to n° pentagonal, and therefore pentagonal are: 1, 5, 12, 22, 35, 51 … pyramids are obtained by making the sum of the first consecutive n squares: 1, 4, 9, 16, 25 … and they are the numbers: 1, 5, 14, 30, 55 … In a similar way the hexagonal numbers are obtained starting from the arithmetic series of reason 4, or series of hexagonal gnomons, which are: 1, 5, 9, 13, 17…; and the hexagons are: 1, 6, 15, 28, 45… It is easy to recognize that the hexagonal n° number is none other than the (2n - 1)° triangular number. It could also be shown that in the homothetic development of pentagons and hexagons the similarity of the form is preserved, but not the isotropy; and therefore, although the plane allows for a division into regular hexagons, its total and isotropic filling cannot be obtained by means of the homothetic development of three congruent hexagons around a common vertex. Thus, it can also be shown that space allows an equipartition only through the cubes, whose vertices fill it totally and isotropically; but it does not consent an equipartition in another way, although the tetrahedron and also the octahedron can be developed homothetically and completely, and isotropically fill the angle within which they develop. We make this observation because Aristotle, after having correctly stated 7) that the plane can be in equipartition only by means of regular triangles, squares, and regular hexagons, adds that space can be equipartitioned by cubes and by pyramids. This is an error Aristotle made; and, since the three regular polyhedral numbers: tetrahedral, cubic, and octahedral, developed homothetically within one of their angleoids [part of space bounded by an indefinite pyramid] fill this angleoid totally and isotropically, Aristotle's error consists in having confused the space with the space of the angleoid; but if the error comes from such confusion, there is indirect proof that the Pythagoreans of the time were already concerned with cubic, tetrahedral and octahedral numbers, as well as with the question of the equipartition of the plane by regular polygons, and of space by regular polyhedra, and in particular of the space contained in a angleoid. In addition to these plane numbers called polygonal numbers, and to the pyramidal numbers represented in space by the polygonal-based pyramids, the Pythagoreans considered plane and solid numbers with a rectangular shape, and parallelepiped and regular polyhedron shapes. The formula that gives the polygonal number n° which has r sides was known to Diophantus and is: As two points are needed to delimit a segment of a straight line, the minimum number of straight lines with which a portion of the plane is delimited is three; of all plane numbers, three is the minimum; similarly, the minimum number of planes needed to delimit a portion of the space is four; among all solid numbers, 4 or the tetrahedron is the minimum. According to Plato (see Timaeus) this tetrahedron, or pyramid, as he calls it, is the last constituent particle of bodies, that is, the atom or molecule of matter. Of course, today we know that atoms or molecules do not have this shape and that they are by no means indivisible, but it is worth noting that the body having the greatest molecular firmness, that is the diamond, has a molecule composed of four atoms arranged in a shape of a regular tetrahedron. 9) Perfection, that is, the completion of the universal manifestation, is reached with the 10, which is the sum of numbers up to four. The decade contains the whole, like the unit, that contains all potentially. The name δεκάς is precisely this for this receptive property δεχάς. The Pythagorean symbol of the tetractys, in its schematic form of an equilateral triangle, clearly coincides with the schematic form of the Masonic delta, and also with the schematic form of the Christian delta, symbol of the Trinity. This latter assimilation is done easily, indeed with carelessness, especially by fitting inside it the eye of the Eternal Father. The Christian character of the Masonic symbol is no longer so conspicuous when, as often happens, the tetragrammaton is written in the triangle, that is, the name of God in four letters, thus designated by the kabbalists with the Greek word; and it even disappears when the triangle is placed within the flaming five-pointed star or Pythagorean pentalpha, as in the title page of Baron De Tschoudy's Etoile Flamboyante, to whom the ritual of the 14th degree of the Scottish Rite is attributed. |
CAPITOLO I La Tetractis pitagorica ed il Delta massonico No, io lo giuro per colui che ha Riesumare e restituire l'antica aritmetica pitagorica è opera quanto mai ardua, perché le notizie che ne sono rimaste sono scarse e non tutte attendibili. Bisognerebbe ad ogni passo ed affermazione citare le fonti e discuterne il valore; ma questo renderebbe la esposizione lunga e pesante e meno facile la intelligenza della restituzione. Perciò, in generale, ci asterremo da ogni apparato filologico, ci atterremo soltanto a quanto resulta meno controverso e dichiareremo sempre quanto è soltanto nostra opinione o resultato del nostro lavoro. 1 + 1 = 2 > 1 . 1; 2 + 2 = 4 = 2 . 2; 3 + 3 = 6 < 3 . 3 Modernamente invece è stato osservato che 1, 2, 3 sono i soli numeri interi positivi la cui somma sia eguale al prodotto. Si può anche riconoscere facilmente che 1, 2, 3 è la sola terna di interi consecutivi per la quale accade che la somma dei primi due è eguale al terzo; infatti l'equazione x + (x + 1) = x + 2 ammette per unica soluzione x = 1. Così pure si riconosce subito mediante la raffigurazione geometrica che la somma di più interi consecutivi supera sempre il numero che segue l'ultimo degli addendi, tranne nel caso in cui gli addendi sono due in cui si ha: 1 + 2 = 3. Concludendo la triade, la santa trinità, si può ottenere solo mediante l'addizione della monade e della diade.
Questo sviluppo geometrico del primo triangolo rispetto ad uno dei tre vertici preso come centro di omotetia, ci dà così successivamente i numeri triangolari; e si chiama gnomone triangolare la base che si aggiunge per passare da un triangolare al triangolare consecutivo. Aritmeticamente, scritta in una prima riga la successione dei numeri interi, se ne deduce la successione dei triangolari, scrivendo l'unità sotto l'unità, poi facendo la somma di uno e di due, eppoi prendendo per elementi della seconda riga i numeri che si ottengono facendo successivamente la somma dei primi numeri interi, oppure facendo, per ottenere un elemento della seconda riga, la somma dell'elemento che lo precede nella stessa riga con quello che lo precede nella stessa colonna:
Esso è perciò un quadrato; è il secondo quadrato, perché l'unità è il quadrato di uno. Lo gnomone del quadrato, ossia la differenza tra il 4 che è il secondo quadrato ed il quadrato precedente è 3, il terzo quadrato, ossia come noi diciamo il quadrato di base 3, si ottiene nella raffigurazione geometrica aggiungendo al di sotto ed a destra uno gnomone a forma di squadra composto di 5 punti; e così via si passa da un quadrato al successivo aggiungendo successivamente i numeri dispari. Si vede così che anche i quadrati crescono conservando la similitudine della forma; e, poiché attorno ad un punto si possono disporre quattro angoli retti congruenti ed in ognuno di essi un quadrato, ne segue che, sviluppando omoteticamente rispetto al vertice comune come centro di omotetia i quattro quadrati, si ottiene il riempimento totale ed isotropico del piano mediante quadrati.
Conducendo di fianco e parallelamente ad una diagonale una linea retta essa divide un numero eteromeco in due parti che sono due triangoli eguali; e siccome il numero dei punti dell'n° eteromeco, costituito da n colonne e da n righe è n (n+ 1) ne segue per l'n° numero triangolare la formola
ricordando la definizione di triangolare si ha:
Se invece si conduce in un numero quadrato la parallela ad una diagonale, il quadrato si suddivide in due triangolari consecutivi; ossia la somma di due triangolari consecutivi è eguale ad un quadrato; e questo permette di dedurre dalla successione dei triangolari quella dei quadrati. Scritta nella prima riga la successione dei triangolari si ottiene nella seconda riga la successione dei quadrati Esiste un solo sviluppo lineare dei numeri. Esistono invece infiniti sviluppi superficiali dei numeri ed infiniti sviluppi solidi. Per esempio il numero 5 si può rappresentare nel piano mediante i 5 vertici di un pentagono e nello spazio mediante i cinque vertici di una piramide a base quadrata. Lo sviluppo per i pentagonali si fa prendendo come centro di omotetia uno dei vertici del pentagono, e per il tetraedro a base quadrata prendendo come centro di omotetia il vertice della piramide. Aritmeticamente per ottenere i pentagonali basta partire dalla successione dei termini della serie aritmetica di ragione tre ossia dai numeri: 1, 4, 7, 10, 13, 16 … e farne la somma. La somma dei primi n è eguale all'n° pentagonale, e quindi i pentagonali sono: 1, 5, 12, 22, 35, 51 … I piramidali a base quadrata si ottengono invece facendo la somma dei primi n quadrati consecutivi: 1, 4, 9, 16, 25 … e sono i numeri: 1, 5, 14, 30, 55 … In simile modo si ottengono i numeri esagonali partendo dalla serie aritmetica di ragione 4, o serie degli gnomoni esagonali che sono: 1, 5, 9, 13, 17 …; e gli esagonali sono: 1, 6, 15, 28, 45… Si riconosce facilmente che l'n° numero esagonale non è altro che il (2n - 1)° numero triangolare. Si potrebbe anche mostrare che nello sviluppo omotetico dei pentagonali e degli esagonali si conserva la similitudine della forma, ma non l'isotropia; e perciò, sebbene il piano acconsenta una ripartizione in esagoni regolari, non se ne può ottenere il riempimento totale ed isotropico mediante lo sviluppo omotetico di tre esagonali congruenti attorno ad un vertice comune. Cosi pure si può mostrare che lo spazio acconsente una equipartizione solo mediante i cubi i cui vertici lo riempiono totalmente ed isotropicamente; ma non acconsente una equipartizione in altro modo sebbene il tetraedro ed anche l'ottaedro siano sviluppabili omoteticamente e riempiano totalmente ed isotropicamente l'angoloide entro il quale si sviluppino. Facciamo questa osservazione perché Aristotile, dopo avere detto7) correttamente che il piano può essere equipartito solo mediante triangoli regolari, quadrati ed esagoni regolari, aggiunge che lo spazio può essere equipartito mediante cubi e mediante piramidi. Si tratta di un errore in cui è incorso Aristotile; e, siccome i tre numeri poliedrici regolari tetraedrico, cubico ed ottaedrico, sviluppati omoteticamente entro uno dei loro angoloidi, riempiono questo angoloide totalmente ed isotropicamente, l'errore di Aristotile consiste nell'avere confuso lo spazio con lo spazio dell'angoloide; ma se l'errore proviene da una tale confusione si ha una prova indiretta che i pitagorici del tempo si occupavano già dei numeri cubici, tetraedrici ed ottaedrici nonché della questione della equipartizione del piano mediante poligoni regolari e dello spazio mediante poliedri regolari ed in particolare dello spazio contenuto in un angoloide. Oltre a questi numeri piani detti numeri poligonali, ed ai numeri piramidali raffigurati nello spazio da delle piramidi a, base poligonale, i pitagorici considerarono numeri piani e solidi a forma rettangolare, e di parallelepipedo ed a forma di poliedro regolare. La formola che dà l'n° numero poligonale che ha r lati era nota a Diofanto ed è Come per delimitare un segmento di retta occorrono due punti, il minimo numero di rette con cui si delimita una porzione di piano è il tre; tra tutti i numeri piani il tre è il minimo; analogamente il minimo numero di piani occorrente per delimitare una porzione dello spazio è quattro; tra tutti i numeri solidi il 4 ossia il tetraedro è il minimo. Secondo Platone (cfr. il Timeo) questo tetraedro o piramide, come egli lo chiama, è l'ultima particella costituente i corpi, ossia l'atomo o molecola della materia. Naturalmente oggi sappiamo che gli atomi o le molecole non hanno questa forma e che non sono affatto indivisibili, ma vale la pena di notare che il corpo che possiede la maggiore saldezza molecolare, ossia il diamante, ha la molecola composta di quattro atomi disposti a forma di tetraedro regolare 9). La perfezione, ossia il completamento della manifestazione universale, è raggiunta col dieci che è la somma dei numeri sino a quattro. La decade contiene il tutto, come l'unità, che contiene il tutto potenzialmente. Il nome δεκάς è appunto questo per tale proprietà ricettiva δεχάς. Il simbolo pitagorico della tetractis, nella sua forma schematica di triangolo equilatero, coincide manifestamente colla forma schematica del delta massonico, ed anche con la forma schematica del delta cristiano simbolo della Trinità. Questa ultima assimilazione vien fatta facilmente, anzi con faciloneria, specialmente schiaffandoci dentro tanto di occhio del Padre eterno. Il carattere cristiano del simbolo massonico non è più tanto appariscente quando; come spesso accade, nel triangolo compare scritto il tetragrammaton, ossia, il nome di Dio in quattro lettere, così designato dai cabalisti con parola greca; e sparisce addirittura quando il triangolo è collocato entro la stella fiammeggiante a cinque punte o pentalfa pitagorico, come nel frontespizio dell'Etoile Flamboyante del Barone De Tschoudy, cui è attribuito il rituale del 14° grado del Rito Scozzese. |
|
CHAPTER II The quatern of composite or synthetic numbers Not from any wood, as Pythagoras said, In the development of numbers starting from the unit and passing through the line segment, triangle, and tetrahedron, we had to stop at the number four because the addition of a new point outside the three-dimensional space is not possible for human intuition. We can continue to consecutively add units, but we can only do so by remaining in the field of linear, plane, and solid numbers; and, considering, for example, linear numbers, there is no criterion for distinguishing the relative properties of the various numbers. We will see later, when dealing with ternary numbering, the archaic reasons that made the number three a perfect number in the classical and Aristotelian meaning of the word. The number nine, the power of three, is also perfect for the same reasons; furthermore, nine is perfect because it is the last digit of a number, and because it is the last number of the quaternion of the composite number contained within the decade. We have thus found that the radius of the circumscribed circumference of an equilateral triangle of height h is equal to two thirds of this height. In a similar way and taking advantage of the isotropy of the regular tetrahedron it is recognized that, if the points constituting the fifth tetrahedral number are arranged so that the bases are regular triangles, they can be arranged in five equidistant planes, of which the first passing through the vertex of the tetrahedron, the second containing three points, the third six, the fourth ten points forming the tetractys, and the fifth the triangular base of the tetrahedron. The center of the tetractys also belongs to the tetrahedral number, and it is intuitively recognized (but it can be shown) that the four heights of the tetrahedron are equal, that they meet at a point which belongs to the four tetractys located above the four bases, and that this center of the tetrahedron divides each height into two parts of which the smaller is 1: 4 of the height, while the greater is 3: 4 of the height. Thus, the radius of the sphere circumscribed to the regular tetrahedron is three times the radius of the inscribed sphere and is 3: 4 of the height of the tetrahedron. The property can be stated by saying that, taking a segment h, the tetractys of height h, and the tetrahedron of height h, the entire segment h and its half are the extremes of a geometric proportion of which the other terms are the radius of the circumscribed circumference to the tetractys, and the radius of the sphere circumscribed to the tetrahedron. Thus considering the tetractys of height h and the tetrahedron of the same height, it happens that the radius of the circumference circumscribed to the tetractys is the harmonic mean of the height and its half, and the radius of the sphere circumscribed to the tetrahedron is the arithmetic mean of the height and its half. |
CAPITOLO II La quaterna dei numeri composti o sintetici Non ex omni ligno, ut Pythagoras Nello sviluppo dei numeri partendo dall'unità e passando per il segmento di retta, per il triangolo e per il tetraedro, ci siamo dovuti fermare al numero quattro perché l'aggiunta di un nuovo punto fuori dello spazio tridimensionale non è possibile per l'intuizione umana. Possiamo seguitare ad aggiungere delle unità consecutivamente, ma possiamo farlo solo restando nel campo dei numeri lineari, piani e solidi; e, considerando ad esempio i numeri lineari, manca ogni criterio per distinguere le proprietà relative dei varii numeri. Vedremo in seguito, occupandoci della numerazione ternaria, le ragioni arcaiche che hanno fatto del tre un numero perfetto nella accezione classica ed aristotelica della parola. Il nove, potenza del tre, è anche esso perfetto per le stesse ragioni; inoltre il nove è perfetto perché ultimo numero di una cifra, e perché è l'ultimo numero della quaterna del numeri composti contenuti entro la decade. Abbiamo così trovato che il raggio della circonferenza circoscritta ad un triangolo equilatero di altezza h è eguale ai due terzi di questa altezza. In modo analogo ed usufruendo della isotropia del tetraedro regolare si riconosce che, se i punti costituenti il quinto numero tetraedrico sono disposti in modo che le basi siano dei triangoli regolari, essi si possono disporre in cinque piani equidistanti, di cui il primo passante pel vertice del tetraedro, il secondo contenente tre punti, il terzo sei, il quarto dieci punti formanti la tetractis, ed il quinto la base triangolare del tetraedro. Il centro della tetractis appartiene anche al numero tetraedrico, e si riconosce intuitivamente (ma si può dimostrare) che le quattro altezze del tetraedro sono eguali, che esse si incontrano in un punto che appartiene alle quattro tetractis situate al di sopra delle quattro basi, e che questo centro del tetraedro divide ogni altezza in due parti di cui la minore è 1 : 4 dell'altezza, mentre la maggiore è i 3 : 4 dell'altezza. Cosi il raggio della sfera circoscritta al tetraedro regolare è il triplo del raggio della sfera inscritta ed è i 3 : 4 dell'altezza del tetraedro. La proprietà si può enunciare dicendo che, presi un segmento h, la tetractis di altezza h e il tetraedro di altezza h, l'intero segmento h e la sua metà sono gli estremi di una proporzione geometrica di cui gli altri termini sono il raggio della circonferenza circoscritta alla tetractis ed il raggio della sfera circoscritta al tetraedro. Considerando quindi la tetractis di altezza h ed il tetraedro di eguale altezza, accade che il raggio della circonferenza circoscritta alla tetractis è la media armonica dell'altezza e della sua metà, ed il raggio della sfera circoscritta al tetraedro è la media aritmetica dell'altezza e della sua metà. |
|
CHAPTER III The triad of odd prime numbers within the decade What are these numbers alluding to? We start from the tetrachord of Philolaus C, F, G, C whose strings have the lengths 1, 3 : 4, 2 : 3, 1 : 2 respectively such that
In the Pythagorean scale, the intervals or ratios of the notes of the octave to the fundamental unit note are expressed in an orderly manner by
and it is easy to recognize that, due to the way in which we preceded the extension of the tetrachord, all these ratios contain only the powers of 2 and 3 in the numerator and denominator. The maximum power of two is 128 = 27 and the maximum power of the three is 243 = 35. The same thing happens considering the ratios between any two notes of the octave. So that while in the tetrachord appear only the ratios of the numbers 1, 2, 3, 4 of the tetractys, in the heptachord there are only the ratios of the powers of the numbers of the tetractys, and precisely the first nine powers of two and the first six powers of three, in addition to the unit, that is, the numbers
In the Pythagorean scale, the five "intervals" or tones between C and D, between D and E, between F and G, between G and A, and between A and B are exactly equal, and in the natural scale they are sensibly equal; and in both scales these intervals are greater than the two remaining intervals between E and F and between B and C. To remedy this drawback, the Pythagoreans inserted five other notes between the major intervals (which correspond to the black keys of the piano) in order to obtain twelve notes, each of which differs from the previous one by a significantly constant interval equal to a semitone. In the temperatescale, introduced by Bach, these intervals are all absolutely equal and the lengths of the twelve strings constitute a geometric progression, but the intervals are no longer expressed by simple ratios, that is, by rational numbers, but by irrational numbers. In the case of stringed instruments, in which the length of the strings is fixed by the fingers and the ear of the player, the physicist Blaserna states that the great virtuosos of the violin tend to prefer the Pythagorean scale to the natural one; but it is somewhat difficult to establish the accuracy of this statement, because only an extremely sensitive ear can perceive the difference. Meanwhile, we note that the development of the tetrachord by fifth has led us to the number seven and, in connection, also to the number twelve.
The triad of consecutive numbers 3, 4, 5 has, therefore, the property that the sum of the squares of the first two is equal to the square of the third. Indeed, it is easy to recognize that this is the only set of consecutive integers that enjoys this property; in fact by indicating with x - 1, x and x + 1 the three consecutive numbers of the equation (x - 1)2 + x2 = (x + 1)2
and we consider the indeterminate equation in the unknown r and x
which, by developing and reducing becomes:
that is
whence
Examples:
an equation which, after the development and reductions becomes:
Giving the y the values 1, 2, 3, 4… the following pairs of solutions are obtained:
and we see that the only integer solution is given by the pair x = 10, y = 6. The problem, therefore, admits the only solution |
CAPITOLO III La terna dei numeri primi dispari entro la decade A che cosa alludono questi numeri? Partiamo dal tetracordo di Filolao do, fa, sol, do le cui corde hanno rispettivamente le lunghezza 1, 3 : 4, 2 : 3, 1 : 2 tali che
Nella scala pitagorica gli intervalli o rapporti delle note dell'ottava alla nota unitaria fondamentale sono espressi ordinatamente da
ed è facile riconoscere che per il modo con cui si è preceduto alla estensione del tetracordo tutti questi rapporti contengono al numeratore ed al denominatore solo delle potenze del due e del tre. La massima potenza del due è il 128 = 27 e la massima potenza del tre è il 243 = 35. La stessa cosa accade considerando i rapporti tra due note qualunque dell'ottava. Cosicché mentre nel tetracordo compaiono solo i rapporti dei numeri 1, 2, 3, 4 della tetractis, nell'eptacordo compaiono solo i rapporti delle potenze dei numeri della tetractis, e precisamente le prime nove potenze del due e le prime sei potenze del tre, oltre all'unità, ossia i numeri
Nella scala pitagorica i cinque «intervalli» o toni tra il do ed il re, tra il il re ed il mi, tra il fa ed il sol, tra il sol ed il la e tra il la ed il si sono esattamente eguali, e nella scala naturale sono sensibilmente eguali; ed in entrambe le scale questi intervalli sono maggiori dei due restanti intervalli tra il mi ed il fa e tra il si ed il do. Per ovviare a questo inconveniente i pitagorici inserirono tra gli intervalli maggiori altre cinque corde (che corrispondono ai tasti neri del pianoforte) in modo da ottenere dodici corde di cui ciascuna differisce dalla precedente di un intervallo sensibilmente costante ed eguale a un semitono. Nella scala temperata, introdotta da Bach, questi intervalli sono tutti assolutamente eguali e le lunghezze delle dodici corde costituiscono una progressione geometrica, ma gli intervalli non sono più espressi da rapporti semplici ossia da numeri razionali ma da numeri irrazionali. Nel caso degli strumenti ad arco, in cui la lunghezza delle corde è fissata dalle dita e dall'orecchio del suonatore, il fisico Blaserna afferma che i grandi virtuosi del violino hanno la tendenza a preferire la scala pitagorica a quella naturale; ma è un po' difficile stabilire la esattezza di questa affermazione perché solo un orecchio estremamente sensibile può percepire la differenza. Constatiamo frattanto che lo sviluppo per quinte del tetracordo ci ha condotto al numero sette ed, in connessione, anche al numero dodici.
La terna dei numeri consecutivi 3, 4, 5 gode dunque della proprietà che la somma dei quadrati dei primi due è eguale al quadrato del terzo. Anzi è facile riconoscere che questa è la sola terna di interi consecutivi che gode di questa proprietà; infatti indicando con x - 1, x e x + 1 tre numeri consecutivi l'equazione
(x - 1)2 + x2 = (x + 1)2
e consideriamo l'equazione indeterminata nelle incognite r ed x
che sviluppando e riducendo diviene:
Ossia
da cui
Esempii:
equazione che dopo lo sviluppo e le riduzioni diviene:
Dando alla y i valori 1, 2, 3, 4… si ottengono le seguenti coppie di soluzioni:
e si vede che l'unica soluzione intera è data dalla coppia x = 10, y = 6. Il problema ammette dunque l'unica soluzione |
|
CHAPTER IV The Pythagorean pentalpha and the flaming star Who ignores geometry shall not enter my school, One of the most important discoveries of the Pythagoreans is that of incommensurable magnitudes and, consequently, of irrational numbers. The simplest case is that of the incommensurability of the diagonal and the side of a square, and Aristotle reports the proof that the Pythagoreans gave. It is a consequence of the Pythagorean Theorem. In fact, if absurdly the diagonal and the side of the square admitted a common measure, that is, if the diagonal contained m times a certain segment and the side contained it n times, the square constructed on the side could be divided into n2 small squares, all equal, and having each side this common segment, and the square constructed on the diagonal could be subdivided into m2m2 small squares equal to them: and being, according to the Pythagorean Theorem, the sum of the squares constructed on the catheti equivalent to the square constructed on the hypotenuse, the number of the small squares 2 n2 contained within the squares of the catheti should be equal to the number of squares m2 of the hypotenuse, that is, it should be
We take the radius OB perpendicular to the radius OA through the center O and, taking the midpoint C of this radius OB, we describe the circle with center C and radius CO: the diameter AC meets this circumference in two points D, E and it happens that the radius OA is mean proportional between the whole secant AE and its external part A D. By dividing this proportion it can be deduced that the external part AD = AM is the golden part of the radius A O. Due to the uniqueness of the golden part, the isosceles triangle with side OA and base AD = AM has a vertex angle of 36° and therefore AM is the side of the inscribed regular decagon; and therefore returning the segment A M as a chord ten times starting from point A, the circumference is divided into ten equal parts; and therefore also in five [parts], taking alternately the points of division. 2) If the radius O A is equal to 1, the radius O C is 1 : 2, the hypotenuse A O of the right-angled triangle, A O C is
and the golden part A D has for measure
Hence, the side of the regular decagon inscribed in the circle with a radius 1 is the golden part of the radius, and has for measure
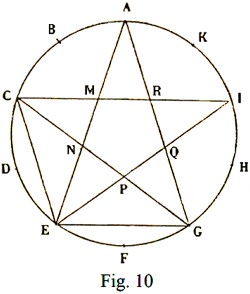
If instead of joining the point A of the division of the circumference into five equal parts with the following point C, the point A is joined with the third division point E, and this with the fifth I and so on, we obtain the starry pentagram, so called because it is composed of five lines, also called pentalpha because it contains five times the letter A formed, for example, by the two strings AE and AG and by the segment MR of the string C I. The term pentalpha is found in the Arithmetic of father Kircher (1665), but the term decal, evidently formed in similarity with the first, is already found in Plutarch. However, this is not what interests us.
Then, since the isosceles triangle CEM has a vertex angle of 36°, the base CM is the golden part of the EC side, and since the five points of the starry pentagram are obviously all equal, it follows that AM = EN is the golden part of EM = A N. Therefore, determined on a segment its golden part, the remaining part is the golden part of the golden part etc., that is AE: AN = AN: EN = EN: NP … In this proportion, each segment is the golden part of the previous one, and it happens as in the proportion of the four strings of the tetrachord that the second segment is the arithmetic mean of the extremes, and the third the harmonic mean of the extremes. Furthermore, just as the Pythagorean range is obtained with the law of fifth from the tetrachord of Philolaus, so each term of the chain of equal relations is obtained by taking the golden part of the previous term, that is, by dividing a circle into ten and five equal parts. A____________M______N____________B Fig. 11 the segment AN = BM is the golden part of AD, the segment AM = BN is the golden part of AN, and the intermediate segment MN is the golden part of the segment A M. These four segments form a tetractys analogous to that formed by the four segments of the side of the pentalpha inscribed in the pentagonal face of the dodecahedron. To use a term of magic, it can be said that both the dodecahedron and its face bear the signature of the same harmony; the harmony of the pentalpha coincides with the harmony of the dodecahedron.
in which each term is the golden part of the previous one; and, therefore, the second term is the arithmetic mean of the extremes, while the third term, i.e., the radius r, is the harmonic mean of the extremes. The dodecahedron therefore enjoys the property: The radius of the circumscribed circumference to the face of the dodecahedron is the harmonic mean between the height of the dodecahedron and the side of the regular decagon inscribed in the face. Matila G. Ghyka calls the golden part the "Nombre d'Or" [golden number]; and this is the title of his main work dedicated to the study of sacred architecture of all times. Music, sculpture and architecture, all arts, conform to the law of universal harmony based on the properties of sacred numbers. Now then, the dodecahedron is the polar polyhedron of the icosahedron and, therefore, has twelve faces which are regular pentagons, it has twenty vertices and thirty edges. Applying the previous subdivision procedure to it, we find that the diameters of the circumscribed circumference of a face passing through the vertices divide it into ten equal right-angled triangles, but if the pentalpha is inscribed on the face, the whole pentagon is subdivided by the sides of the pentalpha and by the diameters passing through the vertices of the pentalpha in thirty right-angled triangles, which this time are not isosceles, are not even the very beautiful right-angled triangles dear to Timaeus (i.e., with the double hypotenuse of the minor cathetus), nor are they all the same or equivalent. On the other hand, the surface of the dodecahedron is thus divided into 360 triangles and, correspondingly, the dodecahedron decomposes into 360 tetrahedra which have them as their base and have the center of the polyhedron as their vertex. Now, 360 is the number of divisions of the twelve signs of the zodiac and is the number of days in the Egyptian year. To understand the importance of these mathematical observations in the eyes of the Pythagoreans and Plato, we must remember: 1st - that for them the triangle is the superficial atom (i.e., the last indivisible part) because it is the polygon having the necessary number of sides sufficient to delimit a portion of the plane, and that, correspondingly, the tetrahedron or pyramid is the solid atom because it is the polyhedron having the necessary and sufficient number of faces to delimit a portion of space. 2nd - That for the very definition of polygonal number, every polygonal number is always the sum of triangular numbers, and, for the definition of pyramidal number, every pyramidal number is the sum of tetrahedral numbers. So it was found that even the five cosmic figures, and in particular the symbol of the universe, were composed of tetrahedra, the entire universe was reduced to a sum of tetrahedral atoms. According to what remains of the Pythagorean geometry, and according to the restoration that we have made of it about ten years ago, the Pythagorean geometry was a more general geometry than the Euclidean and Archimedean geometry, as it was independent of Euclid's postulate of parallels, and rhe postulate of Eudoxus-Archimedes. The starting and ending points were probably the same in the two geometries. In Euclid, however, the intent is purely geometric; while in Pythagoras, even if the development was purely geometric, the intent was certainly not, because the characteristic of Pythagorean philosophy was the ever-present connection of the various sciences with each other and, in particular, of geometry with arithmetic, music and astronomy. For the Pythagoreans and for Plato, geometry was a sacred, esoteric, secret science, just as for the freemasons geometry is the direct art of building and the science of "sacred numbers" known only to them; while Euclidean geometry, breaking all contacts and becoming an end in itself, degenerated into a magnificent profane science. The admirable synthesis of all the sciences and all the arts divined by the genius of Pythagoras disappeared, and the specialization began. Catholicism, unlike the other Christian sects derived from Judaism, has recently added the dogma of the immaculate conception to that of the virginity of Mary: and attaches to these dogmas so much importance that it must be addressed in order to support them in the difficulties inherent in the well-known fact that the Gospel speaks several times of the brothers and sisters of Jesus. The difficulty is overcome by affirming that in the Gospel, and only in the Gospel, the word άδελφός does not mean brother — but cousin. Simple and convenient. The Pythagoreans and the classics, speaking of the Immaculate conception and virginity of the number seven and of Pallas Athena, did not need to support themselves with the acrobatics of hermeneutics: and even to us these fables of paganism do not seem as absurd as the paladins of hagiography The number five or pentalpha is the symbol of harmony, and therefore also the symbol of the Pythagorean brotherhood, as the flaming star is the symbol of the Masonic brotherhood cemented by brotherly love. The Pythagoreans wrote the letters composing the word ύγίεια, i.e., health, at the vertices of the pentalpha, because the harmony of all the elements and all the functions of the body manifests itself as health, and the harmony of all the spiritual elements makes possible health or salvation, understood both in the eschatological sense of Orphism, and in the Pythagorean sense of palingenesis. The number seven is the symbol of wisdom. The two words lodge and mason are not words imported from English or French into Italian. They were in use in Italy since the fourteenth century; those of the Comacine masters [Fraternity] were called loggias, and Florence is full of ancient loggias like that of the Lanzi; the presumed derivation of the word lodge: from the word logos, which in Greek means verb or word, is without foundation and serves only to justify the veneration for the verse of St. John: in principio erat Verbum [In the beginning was the Word]. In architecture, loggia is a technical term that designates an open building, supported by columns or pillars, often built in the upper part of the buildings, for example the theater loggione [gallery], and is, therefore, an appropriate term to designate the Masonic temple supported by twelve columns, which has the sky as rhe vault. |
CAPITOLO IV Il pentalfa pitagorico e la stella fiammeggiante Non entri nella mia scuola chi ignora la geometria, Una delle più importanti scoperte dei pitagorici è quella delle grandezze incommensurabili e conseguentemente dei numeri irrazionali. Il caso più semplice è quello della incommensurabilità della diagonale e del lato di un quadrato, ed Aristotile riporta la dimostrazione che ne davano i pitagorici. Essa è una conseguenza del teorema di Pitagora. Infatti se per assurdo la diagonale ed il lato del quadrato ammettessero una comune misura, se cioè la diagonale contenesse m volte un certo segmento ed il lato lo contenesse n volte, il quadrato costruito sul lato si potrebbe suddividere n2 quadratini tutti eguali ed aventi per lato questo comune segmento, ed il quadrato costruito sulla diagonale si potrebbe suddividere in m2 quadratini eguali ad essi: ed essendo pel teorema di Pitagora la somma dei quadrati costruiti sopra i cateti equivalente al quadrato costruito sopra l'ipotenusa bisognerebbe che il numero dei quadratini 2 n2 contenuti entro i quadrati dei cateti fosse eguale al numero dei quadratini m2 dell'ipotenusa, cioè dovrebbe essere 2 n2 = m2. Ora essendo n ed m due numeri interi, i due numeri della precedente eguaglianza dovrebbero contenere gli stessi fattori primi perché un numero si può decomporre in un unico modo in un prodotto di fattori primi; e questo non è possibile perché m dovrebbe contenere il due e quindi m2 conterrebbe il due un numero pari di volte ed allora anche n dovrebbe contenere il due, n2 lo conterrebbe un numero pari di volte e 2 n2 lo conterrebbe un numero dispari di volte.
Si conduce pel centro O il raggio O B perpendicolare al raggio O A e, preso il punto medio C di questo raggio O B, si descrive il cerchio di centro C e raggio C O: il diametro A C incontra questa circonferenza in due punti D, E ed accade che il raggio O A è medio proporzionale tra l'intiera secante A E e la sua parte esterna A D. Dividendo questa proporzione se ne deduce che la parte esterna A D = A M è la parte aurea del raggio A O. Per l'unicità della parte aurea il triangolo isoscele di lato O A e base A D = A M ha l'angolo al vertice di 36° e quindi A M è il lato del decagono regolare inscritto; e perciò riportando il segmento A M come corda dieci volte a partire dal punto A si divide la circonferenza in dieci parti eguali; e quindi anche in cinque prendendo alternativamente i punti di divisione 2). Se il raggio O A è eguale ad uno, il raggio O C è 1 : 2, l'ipotenusa A O del triangolo rettangolo A O C è
e la parte aurea A D ha per misura
Quindi il lato del decagono regolare inscritto nella circonferenza di raggio uno è la parte aurea del raggio ed ha per misura
Se invece di riunire il punto A di divisione della circonferenza in cinque parti eguali con il punto seguente C si riunisce il punto A col terzo punto di divisione E e questo col quinto I e così via si ottiene il pentagramma stellato così chiamato perché composto di cinque linee, detto anche pentalfa perché contiene cinque volte la lettera A formata ad esempio dalle due corde A E ed A G e dal segmento M R della corda C I. Il termine pentalfa si trova nell'aritmetica del padre Kircher (1665), ma il termine decalca, evidentemente formato a simiglianza del primo, si trova già in Plutarco. Comunque non è questo che ci interessa.
Siccome poi il triangolo isoscele C E M ha l'angolo al vertice di 36°, la base C M è la parte aurea del lato E C, e siccome le cinque punte del pentagramma stellato sono manifestamente tutte eguali ne segue che A M = E N è la parte aurea di E M = A N. Perciò determinata sopra un segmento la sua parte aurea, la parte rimanente è la parte aurea della parte aurea ecc., cioè A E : A N = A N: E N = E N : N P… In questa proporzione ogni segmento è la parte aurea del precedente, ed accade come nella proporzione delle quattro corde del tetracordo che il secondo segmento è la media aritmetica degli estremi ed il terzo la media armonica degli estremi. Inoltre, come la gamma pitagorica si ottiene con la legge di quinta dal tetracordo di Filolao, così ogni termine della catena dei rapporti eguali si ottiene prendendo la parte aurea del termine precedente, ossia mediante la divisione di una circonferenza in dieci e cinque parti eguali. A____________M______N____________B Fig. 11 il segmento A N = B M è la parte aurea di A D, il segmento A M = B N è la parte aurea di A N ed il segmento intermedio M N è la parte aurea del segmento A M. Questi quattro segmenti formano una tetractis analoga a quella formata dai quattro segmenti del lato del pentalfa inscritto nella faccia pentagonale del dodecaedro. Per adoperare un termine della magia si può dire che tanto il dodecaedro quanto la sua faccia portano la segnatura di una stessa armonia; l'armonia del pentalfa coincide con l'armonia del dodecaedro.
in cui, ogni termine è la parte aurea del precedente; e quindi il secondo termine è la media aritmetica degli estremi mentre il terzo termine ossia il raggio r è la media armonica degli estremi. Il dodecaedro gode dunque della proprietà: Il raggio della circonferenza circoscritta alla faccia del dodecaedro è la media armonica tra l'altezza del dodecaedro ed il lato del decagono regolare inscritto nella faccia. Il Matila G. Ghyka chiama la parte aurea le «Nombre d'Or»; ed è questo il titolo della sua opera principale dedicata allo studio dell'architettura sacra di tutti i tempi. La musica, la scultura e l'architettura, le arti tutte, si conformano alla legge dell'armonia universale basata sopra le proprietà dei numeri sacri. Ora il dodecaedro è il poliedro polare dell'icosaedro ed ha pertanto dodici faccie che sono dei pentagoni regolari, ha venti vertici e trenta spigoli. Applicando ad esso il procedimento di suddivisione precedente si trova che i diametri della circonferenza circoscritta ad una faccia passanti per i vertici la suddividono in dieci triangoli rettangoli eguali, ma se nella faccia si inscrive il pentalfa tutto il pentagono viene suddiviso dai lati del pentalfa e dai diametri passanti per i vertici del pentalfa in trenta triangoli rettangoli, i quali questa volta non sono isosceli, non sono neppure i triangoli rettangoli bellissimi cari a Timeo (cioè con l'ipotenusa doppia del cateto minore) e non sono neppure tutti eguali né equivalenti. In compenso la superficie del dodecaedro si suddivide in tal modo in 360 triangoli, e corrispondentemente il dodecaedro si decompone in 360 tetraedri che li hanno per base ed hanno per vertice il centro del poliedro. Ora 360 è il numero delle divisioni dei dodici segni dello zodiaco, ed è il numero dei giorni dell'anno egizio. A ben comprendere l'importanza agli occhi dei pitagorici e di Platone di queste osservazioni matematiche occorre ricordare: 1° - che per essi il triangolo è l'atomo (ossia la parte ultima indivisibile) superficiale perché è il poligono avente il numero di lati necessario e sufficiente a delimitare una porzione di piano, e che corrispondentemente il tetraedro o piramide è l'atomo solido perché è il poliedro avente il numero di faccie necessario e sufficiente a delimitare una porzione di spazio. 2° - Che per la definizione stessa di numero poligonale, ogni numero poligonale è sempre somma di triangolari e per la definizione di numero piramidale ogni numero piramidale è somma di numeri tetraedrici. Sicché si veniva a constatare che anche le cinque figure cosmiche ed in particolare il simbolo dell'universo erano composti di tetraedri, l'intiero universo si riduceva ad una somma di atomi tetraedrici. Secondo quanto resta della geometria pitagorica e secondo la restituzione che ne abbiamo fatta una diecina di anni sono, la geometria pitagorica era una geometria più generale della geometria euclidea e di quella Archimedea in quanto che era indipendente dal postulato di Euclide delle parallele e dal postulato di Eudosso-Archimede. Il punto di partenza e quello di arrivo erano probabilmente gli stessi nelle due geometrie. In Euclide però l'intento è puramente geometrico; mentre in Pitagora, anche se lo svolgimento era puramente geometrico, l'intento non lo era certamente, perché la caratteristica della filosofia pitagorica era la connessione sempre presente delle varie scienze tra loro ed in particolare della geometria con l'aritmetica, la musica e l'astronomia. Per i Pitagorici e per Platone la geometria era, una scienza sacra, esoterica, segreta, come per i liberi muratori la geometria è l'arte regia della edificazione e la scienza dei «numeri sacri» noti solo ad essi; mentre, la geometria euclidea, spezzando tutti i contatti e divenendo fine a sé stessa, degenerò in una magnifica scienza profana. La mirabile sintesi di tutte le scienze e di tutte le arti divinata dal genio di Pitagora scomparve, e cominciò la specializzazione. Il cattolicismo, a differenza delle altre sette cristiane derivate dall'ebraismo, ha recentemente aggiunto il dogma della immacolata concezione il quello della verginità di Maria: ed annette a questi dogmi tanta importanza da affrontare per sostenerli le difficoltà inerenti al fatto ben noto che il Vangelo parla a più riprese dei fratelli e delle sorelle di Gesù. La difficoltà viene superata affermando che nel Vangelo e solo nel Vangelo la parola άδελφός non significa fratello ma cugino. Semplicissimo e comodo. I pitagorici ed i classici, parlando della immacolata concezione e della verginità del numero sette e di Pallade Atena, non avevano bisogno di sostenersi con gli acrobatismi dell'ermeneutica: ed anche a noi queste favole del paganesimo non sembrano così assurde come prenderebbero i paladini dell'agiografia. Il numero cinque o pentalfa è il simbolo dell'armonia, e quindi anche il simbolo della fratellanza pitagorica come la stella fiammeggiante è il simbolo della fratellanza massonica cementata dal brotherly love. I pitagorici scrivevano in corrispondenza dei vertici del pentalfa le lettere componenti la parola ύγίεια, ossia salute, perché l'armonia di tutti gli elementi e di tutte le funzioni del corpo si manifesta come salute e l'armonia di tutti gli elementi spirituali rende possibile la salute o salvezza, intesa sia nel senso escatologico dell'orfismo sia nel senso pitagorico della palingenesi. Il numero sette è il simbolo della sapienza. Le due parole loggia e massone non sono in italiano parole importate dall'inglese o dal francese. Esse erano in uso in Italia sino dal trecento; si chiamavano loggie quelle dei fratelli comacini, e Firenze è piena di antiche loggie come quella dei Lanzi; la presunta derivazione della parola loggia: dalla parola logos che in greco significa verbo o parola è priva di fondamento e serve solo a giustificare la venerazione per il versetto di San Giovanni: in principio erat Verbum. In architettura, loggia è termine tecnico che designa un edificio aperto, retto da colonne o pilastri, costruito spesso nella parte alta degli edifici, per esempio il loggione del teatro, e quindi è termine appropriato per designare il tempio, massonico, sorretto da dodici colonne, che ha per volta il cielo. |
|
CHAPTER V The number and its powers The Pythagoreans assign to God Most High What we have explained so far undoubtedly reconnects to the Pythagorean school, and only to the Pythagorean school. But there are also other more archaic elements, which the Pythagoreans have found, accepted, assimilated, and even exalted, although they are independent of the development of Pythagorean arithmetic, which hinges on the consideration of the tetractys. These elements refer to the number three, its multiples, its powers, and immediately consecutive numbers. |
CAPITOLO V Il numero e le sue potenze I pitagorici assegnano al sommo Dio Quanto abbiamo esposto sin ora si riconnette indubbiamente alla scuola pitagorica e soltanto alla scuola pitagorica. Ma vi sono anche altri elementi più arcaici, che i pitagorici hanno trovato, accettato, assimilato ed anche esaltato, sebbene siano indipendenti dallo sviluppo dell'aritmetica pitagorica che si impernia sulla considerazione delle tetractis. Questi elementi si riferiscono al tre, ai suoi multipli, alle sue potenze ed ai numeri immediatamente consecutivi. |
|
The last two lines of the golden verses are: According to the testimony of Nicomachus, Iamblichus, and Theon, to this ternary classification of even numbers corresponded a pure ternary for odd numbers; but it was transmitted to us in a faulty way. Nicomachus distinguishes: 1st - odd prime numbers; 2nd - secondary and synthetic numbers such as 9, 15, 21, 25, 27, 33… which are products of two or more prime factors, even if not distinct; 3rd - numbers that are secondary and composed in themselves but prime with respect to another number such as 25 and 9. It is clear that the second class contains all the numbers that do not belong to the first, and, in the same example reported by Nicomachus, both 25 and 9 belong to the two classes simultaneously. It is, therefore, necessary to return the Pythagorean ternary classification of odd numbers; and we seem to be able to do it in the following way: By observing that, in the Pythagorean ternary classification, between the unit and the [other] numbers there is only the two; that, similarly, in the classification of rectangular numbers, between the square and the promic there is only the heteromecic (which has only one more point in one of its sides): and that, similarly, in the case of the ternary classification of even numbers, between the equally even number 2n and the unequally even number 2n (2 m + 1) in which with n ≥2 there is only the equally odd 2 (2 m + 1 ) where the factor of two is unique, the ternary classification of the odd numbers was probably as follows: 1st, odd prime numbers; 2nd, powers of prime factors of which at least two distinct; 3rd, powers of a single odd prime with exponent at least equal to two. That is: odd prime numbers a; powers of a single prime an with n at least equal to two; the other cases of odd numbers in which there are at least two distinct prime factors. Other less immediate relationships intercede between the numbers of the quatern: 4, 10, 28, 82. The 28-sided polygon has 350 diagonals or ten times the number of diagonals of the decagon, which has 35. Furthermore, the 28th tetrahedral number is ten times the 28th triangular number; and the tenth triangular number, which is 55, is both the harmonic mean and the ratio of the tenth square-based pyramid, which is 1540, and the fourth hexagonal, which is 28. Similarly, 82 following the perfect number 81, as 28 follows 27, is such that the 82nd tetrahedral is equal to 28 times the triangular 82nd: we, therefore, have the two relations: F (3, 28) = 10 P (3, 28): F (3, 82) = 28 P (3, 82). We observe now that the 36 is the eighth triangular number and, at the same time, the sixth square that's to say we have: We do not know if these properties have already been observed by others, sive Deus, sive Dea [whether god or goddess]. |
Gli ultimi due versi dei versi aurei sono: A questa classificazione ternaria dei numeri pari ne corrispondeva una pure ternaria per i numeri dispari secondo la testimonianza di Nicomaco, di Giamblico e di Teone; ma essa ci è stata trasmessa in modo difettoso. Nicomaco distingue: 1° - i numeri primi dispari; 2° - i numeri secondarii e sintetici come il 9, 15, 21, 25, 27, 33… che sono prodotti di due o più fattori primi anche non distinti; 3° - i numeri che sono secondarii e composti in sé stessi ma primi rispetto ad un altro numero come il 25 ed il 9. È manifesto che la seconda classe contiene tutti i numeri che non appartengono alla prima, e nell'esempio stesso riportato da Nicomaco tanto il 25 che il 9 appartengono alle due classi simultaneamente. Occorre dunque restituire la classificazione ternaria pitagorica dei numeri dispari; e ci sembra di poterlo fare nel seguente modo: Osservando che, nella classificazione ternaria pitagorica, tra l'unità ed il numero vi è solo il due; che analogamente nella classificazione dei numeri rettangolari tra il quadrato ed il promeco vi è solo l'eteromeco (che ha un solo punto in più in uno dei suoi lati): e che analogamente nel caso della classificazione ternaria dei numeri pari tra il numero parimente pari 2n ed il numero imparimente pari 2n (2 m + 1) in cui con n ≥2 vi è soltanto il parimente dispari 2 (2 m + 1) in cui il fattore due è unico, la classificazione ternaria dei numeri dispari doveva probabilmente essere la seguente: 1° numeri primi dispari; 2° potenze di fattori primi di cui almeno due distinti; 3° potenze di un unico primo dispari con esponente almeno eguale a due. Ossia: numeri primi dispari a; potenze di un solo primo an con n almeno eguale a due; gli altri casi di numeri dispari in cui vi sono almeno due fattori primi distinti. Altre relazioni meno immediate intercedono tra i numeri della quaterna.: 4, 10, 28. 82. Il poligono di 28 lati ha 350 diagonali ossia il decuplo del numero delle diagonali del decagono che ne ha 35. Inoltre il 28° numero tetraedrico è il decuplo del 28° numero triangolare; ed il decimo numero triangolare che è 55 è ad un tempo media armonica e rapporto tra il decimo piramidale a base quadrata che è 1540 ed il quarto esagonale che è 28. Analogamente l'82 che segue il numero perfetto 81 come il 28 segue il 27, è tale che l'82° tetraedrico è eguale a 28 volte l'82° triangolare: si hanno dunque le due relazioni: F (3, 28) = 10 P (3, 28) : F (3, 82) = 28 P (3, 82). Osserviamo adesso che il 36 è l'ottavo numero triangolare e nel medesimo tempo il sesto quadrato ossia si ha: Non sappiamo se queste proprietà siano già state osservate da altri, sive Deus, sive Dea. |
|
CHAPTER VI The tripartite table Άεισω συνέτοισι· χετρας
δ΄έπίθεσθε βέβηλοι The three immovable jewels of the Lodge are the rough ashlar, the cubic [perfect] ashlar, and the tracing board, or tripartite table, respectively corresponding to the Apprentice, the Fellow-craft, and the Worshipful Master. This tracing board sometimes bears figures or drawings, sometimes, and more often, it bears the Masonic alphabets in cipher, characterized by the fact that they are composed of square-shaped characters. It is obtained by drawing a pair of parallel lines and cutting them with another pair of lines parallel to each other and perpendicular to the first pair, so that the table is divided into nine parts arranged in three lines and three columns. For this reason, it is clearly called a tripartite board, or, with the ancient name tiercel board. Thus traced, Theon's table coincides with the tripartite table of the freemasons; and, together with the rough ashlar and the cubic [perfect] ashlar, it refers to the construction of temples, which, according to the ritual, is the task of Freemasonry, it recalls that in this construction it is necessary to know the sacred numbers, and furthermore, due to its shape, it indicates that the division into triads is of special importance. Freemasonry, with its ceremonial initiation, appears as a continuation in modern times of the classical mysteries entrusted to a trade corporation specialized in sacred architecture. Its origin is unknown: it is not known to whom to attribute its rituals, its symbolism, in which the Pythagorean elements are intimately linked to those of the operative Masons since ancient times. Is it a historically uninterrupted transmission from the ancient mysteries? For example, from the Pythagorean sect of the Acusmatics or from an ancient trade guild to which elements of an initiatory nature were grafted? Or was the mysteriosophical initiatory character later acquired in an unspecified time by a professional guild as it later happened with Rosicrucian and hermetic elements? What is the time of the Jewish-Christian legend of Hiram and the construction of Solomon's temple? Is the tradition of the St. John Freemasonry [blue lodges] connected with the movements of the medieval heresy or is it antecedent? All questions that await an answer. However, the numerical and geometric symbolism of Freemasonry is the Pythagorean one, and, since it is free from any Christian coloring, it may be that the fusion of the symbolism of trade and Pythagorean symbolism goes back to any post-Pythagorean period, and it is certainly not a recent innovation, but one with a very ancient characteristic. |
CAPITOLO VI La tavola tripartita Άεισω συνέτοισι· χετρας
δ΄έπίθεσθε βέβηλοι I tre gioielli immobili della Loggia sono la pietra grezza, la pietra, cubica e la tavola da tracciare, o tavola tripartita, rispettivamente corrispondenti al novizio, al compagno ed al maestro venerabile. Questa tavola da tracciare, o da disegnare, porta talvolta delle figure o disegni, tal'altra, e più spesso, porta gli alfabeti massonici in cifra, caratterizzati dal fatto che sono composti da caratteri a forma quadrata. Essa si ottiene tracciando una coppia di rette parallele e tagliandole con un'altra coppia di rette parallele tra loro e perpendicolari alla prima coppia, di modo che la tavola viene suddivisa in nove parti disposte in tre linee ed in tre colonne. Per questa ragione, manifestamente, è chiamata tavola tripartita, o, con antica denominazione tiercel board. Così tracciata, la tavola di Teone coincide con la tavola tripartita dei liberi muratori; e, insieme alla pietra grezza ed alla pietra cubica si riferisce alla costruzione dei templi, che secondo il rituale è il compito della massoneria, essa ricorda che in questa costruzione occorre la conoscenza dei numeri sacri, ed inoltre per la sua forma indica che la divisione in terne è di speciale importanza. La massoneria con la sua iniziazione cerimoniale si presenta come una continuazione nei tempi moderni dei misteri classici, affidata ad una corporazione di mestiere specializzata nell'architettura sacra. Se ne ignora l'origine: non si sa a chi attribuire i suoi rituali, il suo simbolismo, nei quali gli elementi pitagorici si trovano intimamente legati a quelli muratorii di mestiere sin dai tempi più antichi. Si tratta di una trasmissione storicamente ininterrotta dagli antichi misteri? Per esempio dalla setta pitagorica degli Acusmatici o da una antica corporazione di mestiere cui erano innestati elementi di carattere iniziatico? Oppure il carattere iniziatico misteriosofico è stato acquisito posteriormente in un tempo imprecisato da una corporazione di mestiere come più tardi avvenne con elementi rosacroce ed ermetici? A che tempo risale la leggenda ebraico-cristiana di Hiram e della costruzione del tempio di Salomone? La tradizione della Massoneria di San Giovanni è connessa coi movimenti dell'eresia medioevale od è antecedente? Tutte questioni che attendono una risposta. Comunque sia il simbolismo numerico e geometrico della massoneria è quello pitagorico e siccome è esente da ogni colorazione cristiana può darsi che la fusione del simbolismo di mestiere e del simbolismo pitagorico risalga ad un periodo qualunque post-pitagorico, e certamente non si tratta di innovazione recente ma di caratteristica assai antica. |
|
CHAPTER VII The Great Work and the Palingenesis From sight to sight up to the most beautiful. We have seen that Freemasonry, according to its Statutes and tradition, has as its goal the perfecting of the single human individual. The manuscript of the Bodleian Library, attributed to Henry VI of England, states that "Freemasonry is the knowledge of nature and the individual forces that are in it." The perfection of man is linked to the knowledge or recognition of human nature and the inherent possibilities. It is, therefore, necessary to implement the ancient precept of the Delphic oracle: know thyself; it is necessary to investigate within ourselves the mystery of being, to consider human life, its functions, its limits, and the possibilities of overcoming them, to actively intervene in its progress without abandoning it adrift, to discover and reawaken its latent germs, its senses and powers still unknown, dormant or occult. It is necessary to carry out a work of spiritual edification, a transmutation, conseguir virtute e conoscenza [to pursue virtue and knowledge], so that the worm crawling on the earth forms the angelic butterfly that flies to justice without impediments. It is necessary to build, and not only to pray or worship, or observe, it is necessary to experiment and speculate; and to build upon secure and firm foundations, and not upon beliefs, prejudices, and illusions. The legend of Hiram was also fortunate in the literary field because it was revived and developed by the writer Gérard De Nerval, who, in his Voyage en Orient makes him become a rival of Solomon, and embody the democratic spirit called to triumph over royalty. The existence of pure and simple alchemists who in good faith deluded themselves that they were hermetists does not justify the superficial belief of contemporary science that reduces all hermeticism to alchemy, and after this hasty confusion and conclusion, it makes fun of what it does not know. Similarly, at the time of the "Fedeli d'amore," there were simple poets in the vernacular persuaded that they belonged to the elite group of rhymers "of the dolce stil nuovo," who, under the veil of strange verses, and in a covert hidden language, sang of love, of Beatrice, Laura, Fiammetta, and similar other women: and Dante laughs at them. The contemporary culture that makes a whole bundle of hermetists and alchemists behaves with equal intelligence compared to the vernacular literature of the first centuries; literary and religious prejudices prevent the understanding which is in itself difficult for the layman due to the constant use of allegorical language. And as if these obfuscating factors weren't enough, psychoanalysis has also come forward pretending to interpret the literature of love, the Divine Comedy, and the writings of the Rosicrucians and hermetists, explaining with the same meter and symbolism the occult meaning, for example, of Dante and Stecchetti. These psychoanalytic writers, who see everywhere the inner constellations in a perpetual and unconscious search for a discharge, do not realize that they are the real slaves of the sexual complex, they, who systematically smell and pursue sexual and pornographic obsession everywhere, as the dung beetle pursues and rolls up its favorite raw material. It seems, therefore, that Pythagoras taught the doctrine of metempsychosis or transmigration of souls, but we do not know if this doctrine was faithfully transmitted and it can be deduced, for example, from the exposition that Virgil and Ovid make of it. However, palingenesis and transmigration are two distinct words and concepts. On the other hand, the Golden Verses, which although a late neo-Pythagorean compilation of the Alexandrian period, faithfully reflecting the ancient Pythagorean doctrine, explicitly and emphatically affirm that the final result of the catharsis and the asceticism of the disciple is the attainment of immortality. This is the palingenesis that the last two verses of the Golden Verses categorically promise the disciple that he can leave the body and rise to the free ether. Palingenesis is, therefore, the birth into immortal and divine life, while the first birth grants only the entrance into human life, otherwise the palingenesis would become superfluous. And, since the Golden Verses were addressed to the humanly living disciple, they summarize what to do by saying that, once leaving the body to itself, it is necessary to reach consciously, soul and spirit, up to the free ether, that is, beyond the enveloping enclosure (the periekon or empireo). Passing from human time to psychic time, the difficulty of reuniting the beginning with the end becomes surmountable; and the two problems of immortality and time interpenetrate. Dante treats the question just in this way. He calls the tenth heaven the quiet [calm, immobile] heaven (Convivio. II, 13, Paradise. XXX, 52), that is, the empyrean or sphere of fire, and, while this heaven is calm, the other nine spheres admit movement. Dante is connected to the Aristotelian and Ptolemaic conception; but also, according to the Pythagoreans, it is the movement, the oscillation, the vibration that imprints the succession of time in the cosmos; time sets itself in motion and flows in the fleeting moment between a past that is no longer and a future that not yet is. The holy city is only in this calm heaven; and it is here that Beatrice leads Dante and tells him: THE END |
CAPITOLO VII La Grande Opera e la Palingenesi Di vista in vista infino alla più bella. Abbiamo veduto che la Massoneria, secondo i suoi Statuti e la tradizione, ha per fine il perfezionamento del singolo individuo umano. Il manoscritto della biblioteca Bodleyana, attribuito ad Enrico VI d'Inghilterra, afferma che «la massoneria è la conoscenza della natura e delle singole forze che sono in essa». Il perfezionamento dell'uomo è legato alla conoscenza od al riconoscimento della natura umana e delle inerenti possibilità. Occorre quindi attuare l'antico precetto dell'oracolo di Delfo: conosci te stesso; occorre indagare entro di noi il mistero dell'essere, considerare la vita umana, le sue funzioni, i suoi limiti e le possibilità di superarli, intervenire attivamente nel suo andamento non abbandonandola alla deriva, scoprirne e ridestarne i germi latenti, i sensi e poteri ancora ignoti, dormienti od occulti. Occorre compiere un'opera di edificazione spirituale, una trasmutazione, conseguir virtute e conoscenza, sì che il verme strisciante in terra formi l'angelica farfalla che vola alla giustizia senza schermi. Occorre costruire e non soltanto pregare od adorare, oppure osservare, sperimentare e speculare; e costruire sopra fondamenta sicure e salde e non sopra credenze, pregiudizii ed illusioni. La leggenda di Hiram ha avuto anche fortuna nel campo letterario perché è stata ripresa e sviluppata dallo scrittore Gérard De Nerval, che nel suo Voyage en Orient lo fa divenire un rivale di Salomone ed impersonare lo spirito democratico chiamato a trionfare della regalità. La esistenza degli alchimisti puri e semplici che in buona fede si illudevano di essere degli ermetisti non giustifica la superficiale credenza della scienza contemporanea che riduce tutto l'ermetismo ad alchimia, e dopo questa affrettata confusione e conclusione si fa beffa di ciò che non conosce. In simil modo al tempo dei «Fedeli d'amore» vi furono dei semplici poeti in volgare persuasi di appartenere senza altro alla eletta schiera dei rimatori «del dolce stil nuovo», la quale sotto il velame delli versi strani ed in linguaggio chiuso cantava d'amore, di Beatrice, Laura, Fiammetta e simili altre donne: e Dante li deride. La cultura contemporanea che fa tutto un fascio degli ermetisti e degli alchimisti si comporta con pari intelligenza rispetto alla letteratura in volgare dei primi secoli; pregiudizi letterarii e religiosi ne impediscono la comprensione già di per sé stessa difficile al profano dall'uso costante del linguaggio allegorico. E come se questi fattori di offuscamento non bastassero si è fatta avanti anche la psicoanalisi che pretende interpretare la letteratura d'amore, la Divina Commedia, e gli scritti dei Rosacroce e degli ermetisti, spiegando con lo stesso metro e simbolismo il senso occulto per esempio di Dante e dello Stecchetti. Non si accorgono questi scrittori psicoanalisti, che vedono dappertutto le costellazioni interiori in perpetua ed inconscia ricerca di una scarica, non si accorgono di essere proprio essi i veri schiavi del complesso sessuale, essi che sistematicamente subodorano e perseguono dappertutto l'ossessione sessuale e pornografica come lo scarabeo stercorario persegue ed appallottola la prediletta materia prima. Pare quindi che Pitagora insegnasse la dottrina della metempsicosi o trasmigrazione delle anime, ma non sappiamo se questa dottrina sia stata trasmessa fedelmente e si possa ad esempio desumere dalla esposizione che ne fanno Virgilio ed Ovidio. Comunque palingenesi e trasmigrazione sono due parole e due concetti distinti. D'altra parte i Detti aurei, che per quanto siano una tarda compilazione neo-pitagorica del periodo alessandrino, rispecchiano fedelmente la dottrina pitagorica antica, affermano esplicitamente ed enfaticamente che il risultato finale della catarsi e della ascesi del discepolo è il conseguimento della immortalità. Questa è la palingenesi che gli ultimi due versi dei Detti aurei promettono categoricamente al discepolo che sappia lasciare il corpo ed elevarsi sino al libero etere. La palingenesi è dunque la nascita alla vita immortale e divina, mentre la prima nascita accorda soltanto l'ingresso alla vita umana, altrimenti la palingenesi diverrebbe superflua. E, siccome i Detti aurei erano rivolti al discepolo umanamente vivente, essi riassumono il da fare dicendo che, abbandonato il corpo a sé stesso, occorre pervenire coscientemente, anima e spirito, sino al libero etere, cioè oltre la fascia dell'avviluppante (il periekon o empireo). Passando dal tempo umano al tempo psichico la difficoltà di riunire il principio con la fine diviene superabile; ed i due problemi della immortalità e del tempo si compenetrano. Dante tratta la questione proprio in questo modo. Egli chiama cielo quieto (Conv. II, 13, Par. XXX, 52) il decimo cielo, ossia l'empireo o sfera, del fuoco, e, mentre questo cielo è quieto, le altre nove sfere ammettono il movimento. Dante si collega alla concezione aristotelica e tolemaica; ma anche secondo i pitagorici è il movimento, l'oscillazione, la vibrazione che stampa nel cosmo la successione del tempo; il tempo si pone in movimento e fluisce nell'attimo fuggente tra un passato che non è più ed un futuro che non è ancora. La città santa è soltanto in questo cielo quieto; ed è qui che Beatrice trae Dante e gli dice: Τ Ε Λ Ο Σ |
![]()

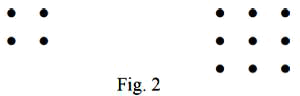

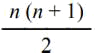
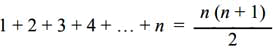
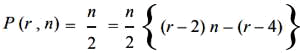
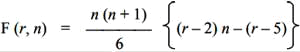
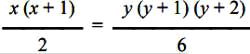
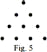
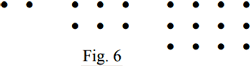
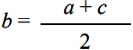
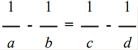
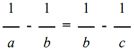
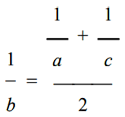
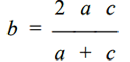
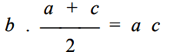
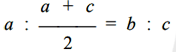
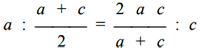
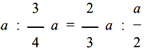
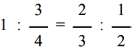

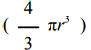

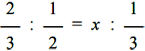
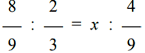
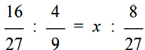
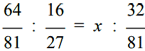
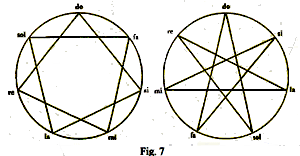


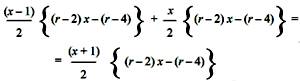
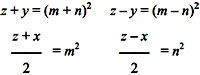
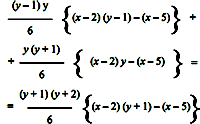

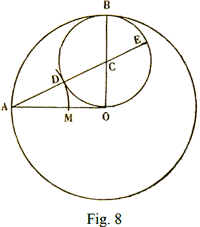
 The regular pentagon, and thus also the decagon and the pentalpha, can also be built without a compass starting from a strip with parallel sides. Just tie it and pull it as you do for a tie knot. It can be easily recognized and shown that it folds up according to three equal segments A B, C D, E A and the two segments D E and C B are also equal to the other three. The strip comes out from the parts of the sides D E and C B of the pentagon, and there is the figure of a bishop's miter (the figure of the bishop in the game of chess) or also of the apron of the fellowcraft. The notched ribbon, or chain of union, which is wrapped and knotted around the columns of the temple, which are ten by removing the two columns at the entrance to the temple, forms ten of these pentagonal nodes, like the ten matching regular pentagons circumscribed to a regular decagon.
The regular pentagon, and thus also the decagon and the pentalpha, can also be built without a compass starting from a strip with parallel sides. Just tie it and pull it as you do for a tie knot. It can be easily recognized and shown that it folds up according to three equal segments A B, C D, E A and the two segments D E and C B are also equal to the other three. The strip comes out from the parts of the sides D E and C B of the pentagon, and there is the figure of a bishop's miter (the figure of the bishop in the game of chess) or also of the apron of the fellowcraft. The notched ribbon, or chain of union, which is wrapped and knotted around the columns of the temple, which are ten by removing the two columns at the entrance to the temple, forms ten of these pentagonal nodes, like the ten matching regular pentagons circumscribed to a regular decagon.